GitHub

TableTransforms.jl

Transforms and pipelines with tabular data.

Overview

This package provides transforms that are commonly used in statistics and machine learning. It was developed to address specific needs in feature engineering and works with general Tables.jl tables.

Past attempts to model transforms in Julia such as FeatureTransforms.jl served as inspiration for this package. We are happy to absorb any missing transform, and contributions are very welcome.

Features

  • Transforms are revertible meaning that one can apply a transform and undo the transformation without having to do all the manual work keeping constants around.

  • Pipelines can be easily constructed with clean syntax (f1 → f2 → f3) ⊔ (f4 → f5), and they are automatically revertible when the individual transforms are revertible.

  • Branches of a pipeline and colwise transforms are run in parallel using multiple processes with the Distributed standard library.

  • Pipelines can be reapplied to unseen "test" data using the same cache (e.g. constants) fitted with "training" data. For example, a ZScore relies on "fitting" μ and σ once at training time.

Rationale

A common task in statistics and machine learning consists of transforming the variables of a problem to achieve better convergence or to apply methods that rely on multivariate Gaussian distributions. This process can be quite tedious to implement by hand and very error-prone. We provide a consistent and clean API to combine statistical transforms into pipelines.

Although most transforms discussed here come from the statistical domain, our long term vision is more ambitious. We aim to provide a complete user experience with fully-featured pipelines that include standardization of column names, imputation of missing data, and more.

Usage

Consider the following table and its pairplot:

using TableTransforms
using CairoMakie, PairPlots

# example table from PairPlots.jl
N = 100_000
a = [2randn(N÷2) .+ 6; randn(N÷2)]
b = [3randn(N÷2); 2randn(N÷2)]
c = randn(N)
d = c .+ 0.6randn(N)
table = (; a, b, c, d)

# pairplot of original table
table |> pairplot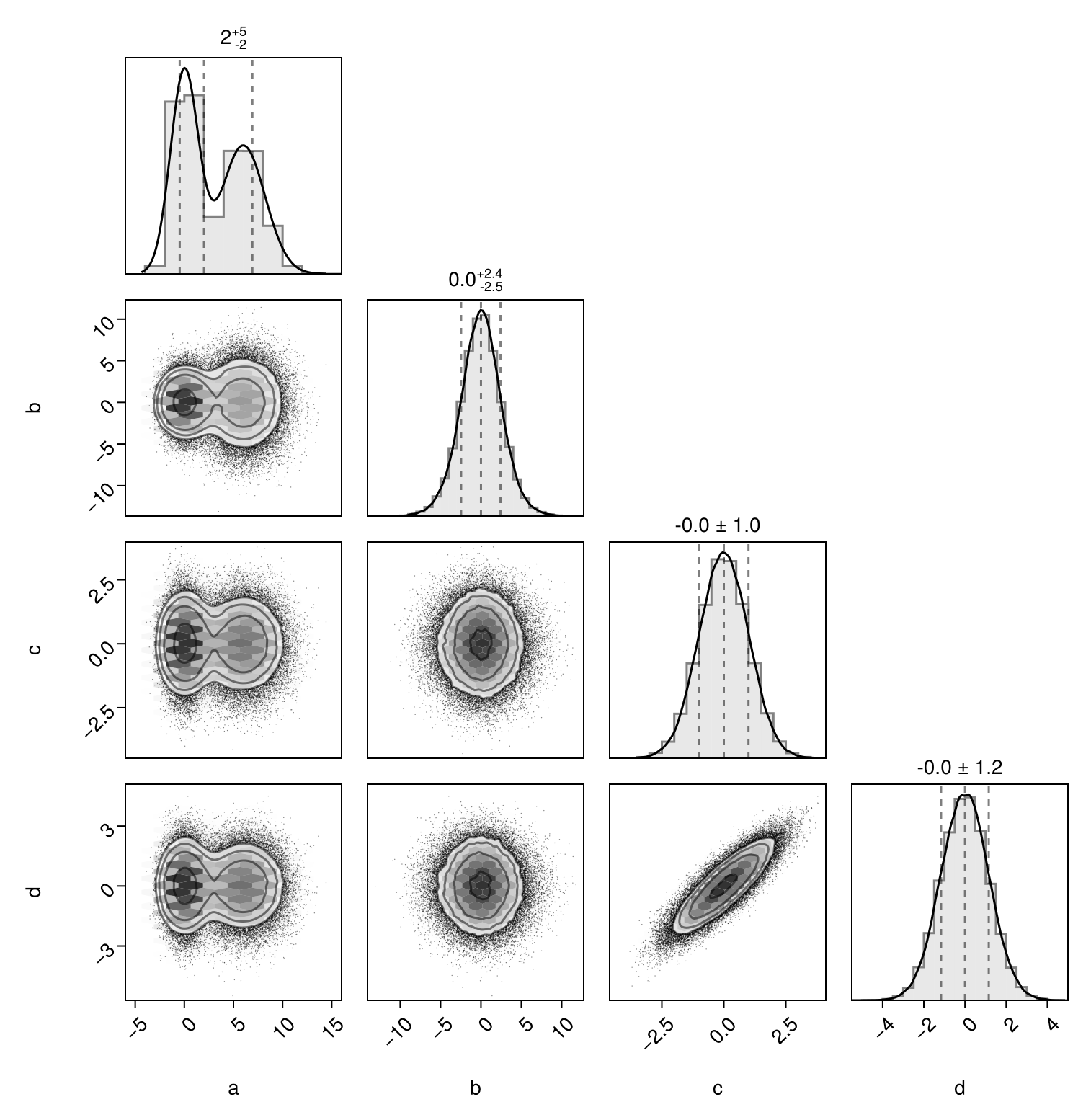
Example block output

We can convert the columns to PCA scores:

# convert to PCA scores
table |> PCA() |> pairplot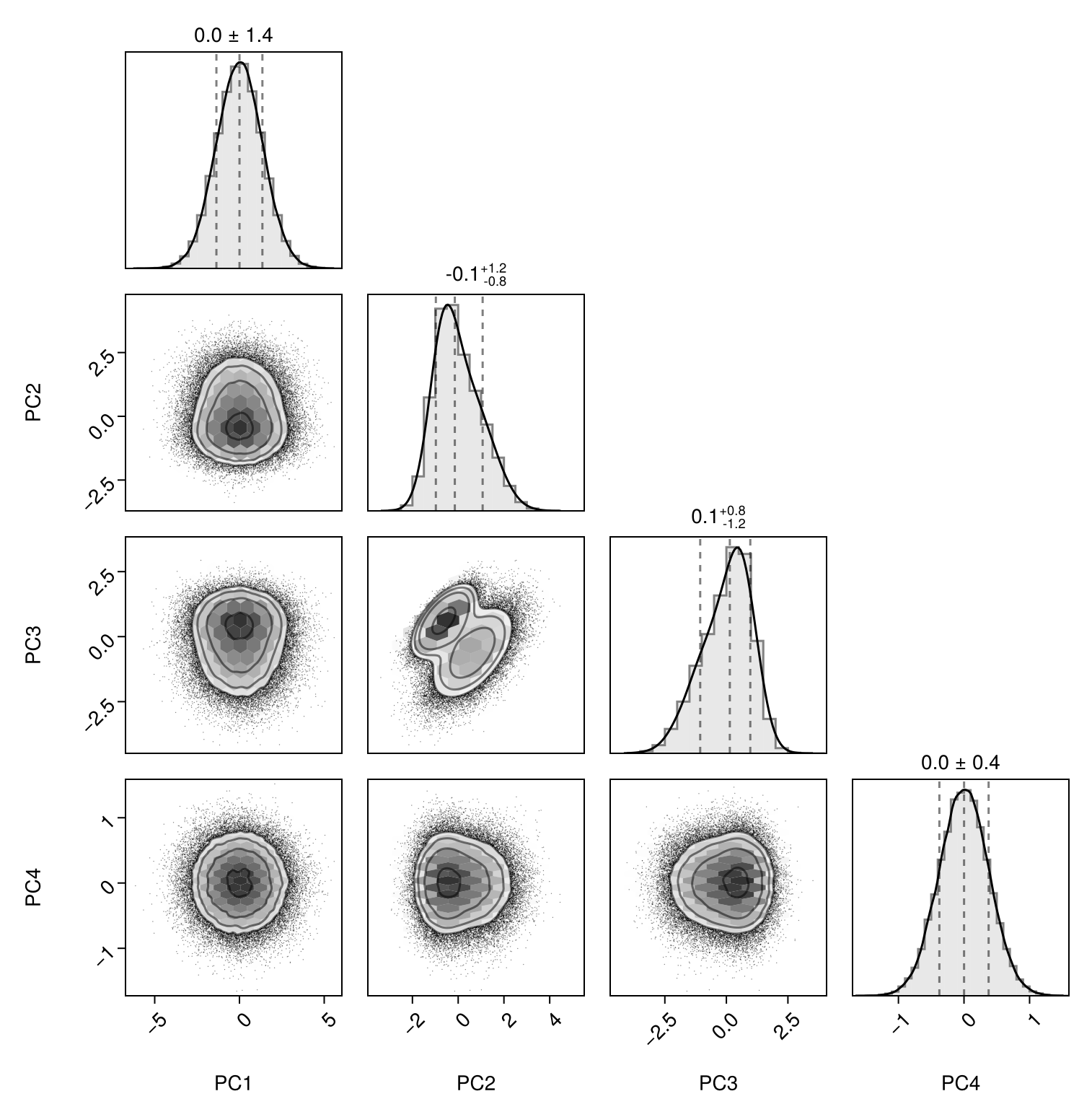
Example block output

or to any marginal distribution:

using Distributions

# convert to any Distributions.jl
table |> Quantile(dist=Normal()) |> pairplot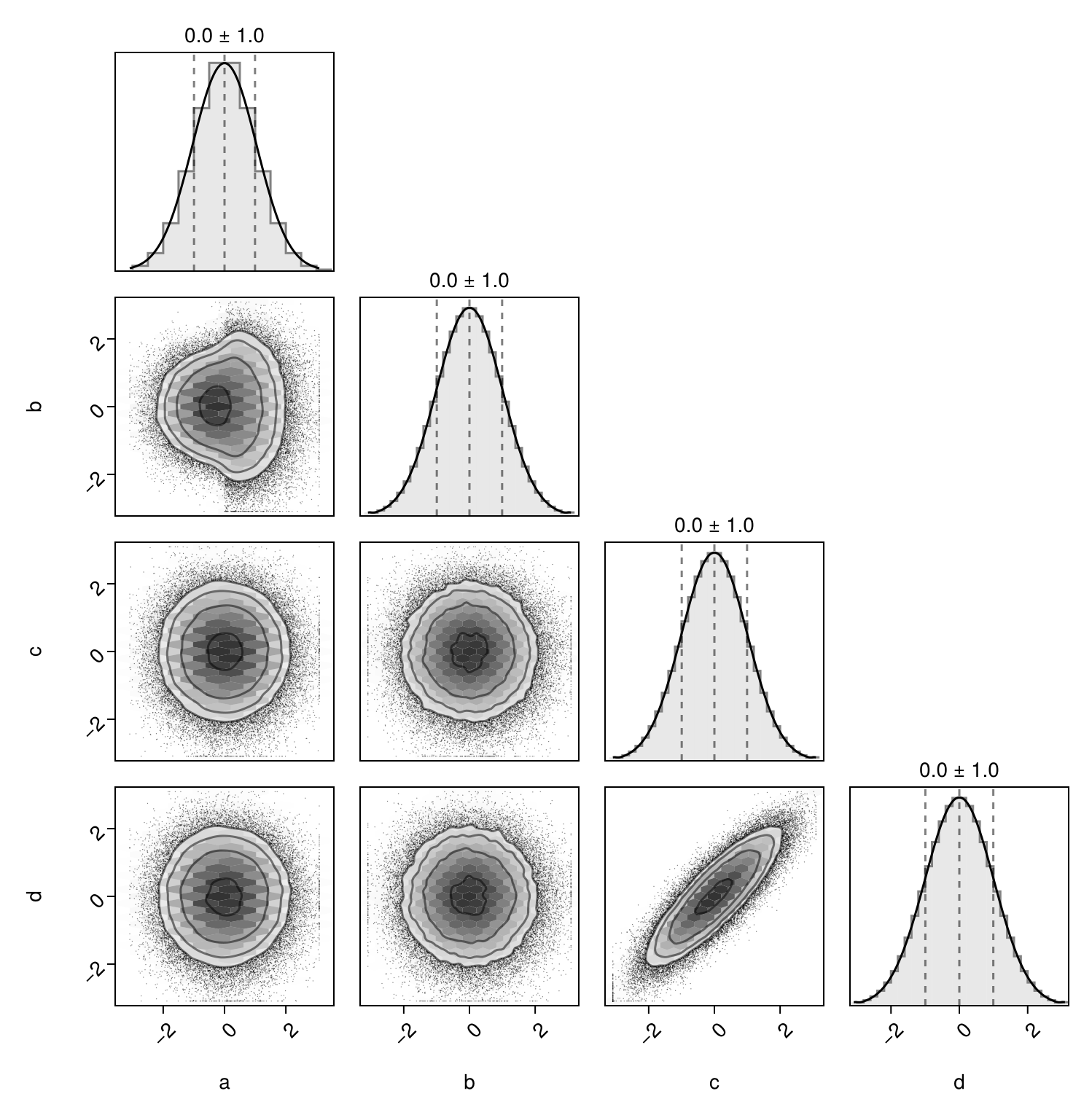
Example block output

Below is a more sophisticated example with a pipeline that has two parallel branches. The tables produced by these two branches are concatenated horizontally in the final table:

# create a transform pipeline
f1 = ZScore()
f2 = LowHigh()
f3 = Quantile()
f4 = Functional(cos)
f5 = Interquartile()
pipeline = (f1 → f2 → f3) ⊔ (f4 → f5)

# feed data into the pipeline
table |> pipeline |> pairplot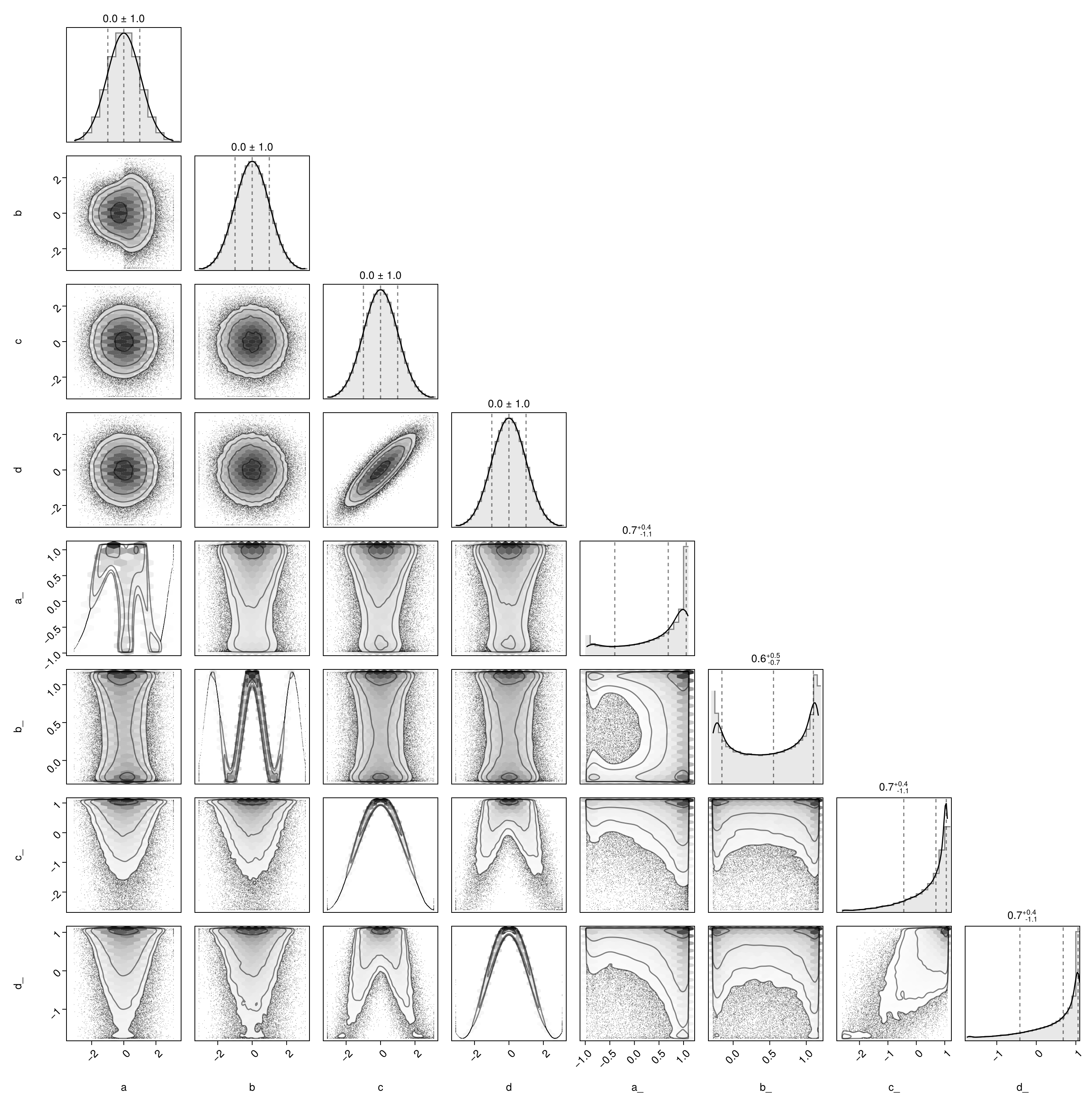
Example block output

Each branch is a sequence of transforms constructed with the → (\to<tab>) operator. The branches are placed in parallel with the ⊔ (\sqcup<tab>) operator.

TableTransforms.ParallelTableTransform — Type
ParallelTableTransform(transforms)

A transform where transforms are applied in parallel. It isrevertible if any of the constituent transforms is revertible. In this case, the revert is performed with the first revertible transform in the list.

Examples

LowHigh(low=0.3, high=0.6) ⊔ EigenAnalysis(:VDV)
ZScore() ⊔ EigenAnalysis(:V)

Notes

  • Metadata is transformed with the first revertible transform in the list of transforms.
source

Reverting transforms

To revert a pipeline or single transform, use the apply and revert functions instead. The function isrevertible can be used to check if a transform is revertible.

TransformsBase.apply — Function
newobject, cache = apply(transform, object)

Apply transform on the object. Return the newobject and a cache to revert the transform later.

source
TransformsBase.revert — Function
object = revert(transform, newobject, cache)

Revert the transform on the newobject using the cache from the corresponding apply call and return the original object. Only defined when the transform isrevertible.

source
TransformsBase.isrevertible — Function
isrevertible(transform)

Tells whether or not the transform is revertible, i.e. supports a revert function. Defaults to false for new transform types.

Transforms can be revertible and yet don't be invertible. Invertibility is a mathematical concept, whereas revertibility is a computational concept.

See also isinvertible.

source

To exemplify the use of these functions, let's create a table:

a = [-1.0, 4.0, 1.6, 3.4]
b = [1.6, 3.4, -1.0, 4.0]
c = [3.4, 2.0, 3.6, -1.0]
table = (; a, b, c)
(a = [-1.0, 4.0, 1.6, 3.4], b = [1.6, 3.4, -1.0, 4.0], c = [3.4, 2.0, 3.6, -1.0])

Now, let's choose a transform and check that it is revertible:

transform = Center()
isrevertible(transform)
true

We apply the transformation to the table and save the cache in a variable:

newtable, cache = apply(transform, table)
newtable
(a = [-3.0, 2.0, -0.3999999999999999, 1.4], b = [-0.3999999999999999, 1.4, -3.0, 2.0], c = [1.4, 0.0, 1.6, -3.0])

Using the cache we can revert the transform:

original = revert(transform, newtable, cache)
(a = [-1.0, 4.0, 1.6, 3.4], b = [1.6, 3.4, -1.0, 4.0], c = [3.4, 2.0, 3.6, -1.0])

Inverting transforms

Some transforms have an inverse that can be created with the inverse function. The function isinvertible can be used to check if a transform is invertible.

TransformsBase.isinvertible — Function
isinvertible(transform)

Tells whether or not the transform is invertible, i.e. whether it implements the inverse function. Defaults to false for new transform types.

Transforms can be invertible in the mathematical sense, i.e., there exists a one-to-one mapping between input and output spaces.

See also inverse, isrevertible.

source

Let's exemplify this:

a = [5.1, 1.5, 9.4, 2.4]
b = [7.6, 6.2, 5.8, 3.0]
c = [6.3, 7.9, 7.6, 8.4]
table = (; a, b, c)
(a = [5.1, 1.5, 9.4, 2.4], b = [7.6, 6.2, 5.8, 3.0], c = [6.3, 7.9, 7.6, 8.4])

Choose a transform and check that it is invertible:

transform = Functional(exp)
isinvertible(transform)
true

Now, let's test the inverse transform:

invtransform = inverse(transform)
invtransform(transform(table))
(a = [5.1, 1.5, 9.4, 2.4], b = [7.6, 6.2, 5.8, 3.0], c = [6.3, 7.9, 7.6, 8.4])

Reapplying transforms

Finally, it is sometimes useful to reapply a transform that was "fitted" with training data to unseen test data. In this case, the cache from a previous apply call is used:

TransformsBase.reapply — Function
newobject = reapply(transform, object, cache)

Reapply the transform to (a possibly different) object using a cache that was created with a previous apply call. Fallback to apply without using the cache.

source

Consider the following example:

traintable = (a = rand(3), b = rand(3), c = rand(3))
testtable  = (a = rand(3), b = rand(3), c = rand(3))

transform = ZScore()

# ZScore transform "fits" μ and σ using training data
newtable, cache = apply(transform, traintable)

# we can reuse the same values of μ and σ with test data
newtable = reapply(transform, testtable, cache)
(a = [3.664372586770125, 1.3010543105102819, 0.20659622020787544], b = [0.34718775148637704, -0.26274719825965603, 1.2490776324474353], c = [0.33062949892284726, 1.4746576094403234, 0.04883085864213076])

Note that this result is different from the result returned by the apply function:

newtable, cache = apply(transform, testtable)
newtable
(a = [1.0979486034606596, -0.23932668246111835, -0.8586219209995408], b = [-0.12795001946747547, -0.929866825966845, 1.0578168454343209], c = [-0.38061724707911765, 1.1344208432568101, -0.7538035961776925])